先日、テスト返却を行いました。
返却すると、生徒たちは平均点に対して「高いな!」や「低い〜!」のような反応をします。教員の間でも平均点に対して「イマイチな平均点だった」や「今回の平均点はXX点で良かった」のような会話が聞かれます。
また、60点がなければ平均点が低かったや、それを超えていれば今回の平均点は高かったというように、何故か平均点60点というのが「正しい」基準のように考えている人がいます。
平均点とはそもそも何なのでしょうか。また、平均点だけをテストの判断材料にしていいのでしょうか。定期試験の平均点には望ましい点数があるのでしょうか。
今日の投稿では平均点について考えたいと思います。
平均とは?
そもそもの話ですが、平均(値)とは何でしょうか。
総務省統計局の「なるほど統計学園」では、平均は「変量の総和を個数で割ったもの」と言われています。難しい言い方をしていますが、つまりは、集めたデータの数値を全て足したものをその個数で割るということです。
平均が同じなのに?
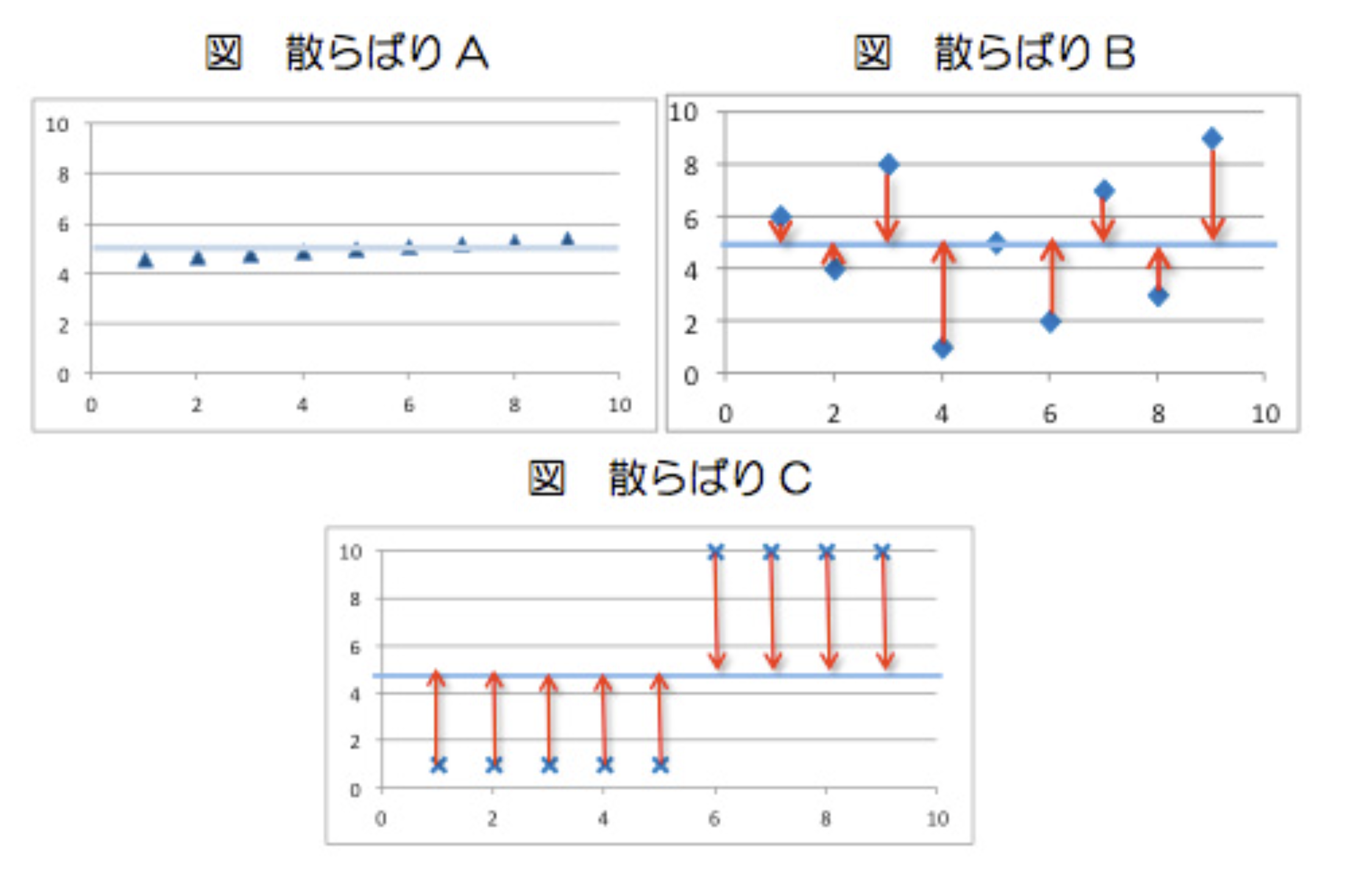
平均については皆さんはよくご存知だと思います。では、下の図を見てみましょう。
下記の図はそれぞれ様々な図になっていますが、実は全て平均が5になります。同じ平均5だとしても図の内容は大きく変わりますよね。
出典:「なるほど統計学園」https://www.stat.go.jp/naruhodo/10_tokucho/chirabari.html
平均以外の分析材料
これらを詳しくみていくために、平均以外にもデータを分析する材料として、ここでは偏差と分散、標準偏差を紹介したいと思います。色々な書籍やHPでは、計算方法等が書かれていますが、この投稿ではその数値によって何を指すことができるかに絞って話したいと思います。
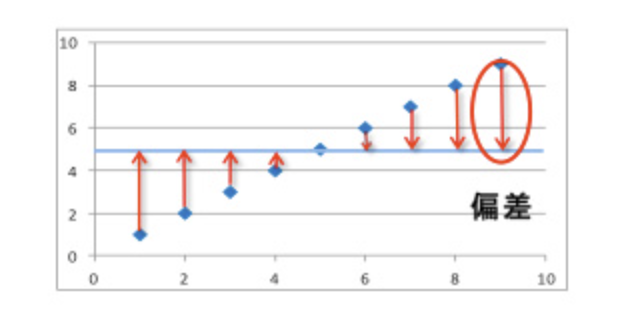
偏差
偏差は、個々の数値と平均の差を表し、その数値が大きければ大きいほど、平均から離れていることを示します。
出典:「なるほど統計学園」https://www.stat.go.jp/naruhodo/10_tokucho/chirabari.html
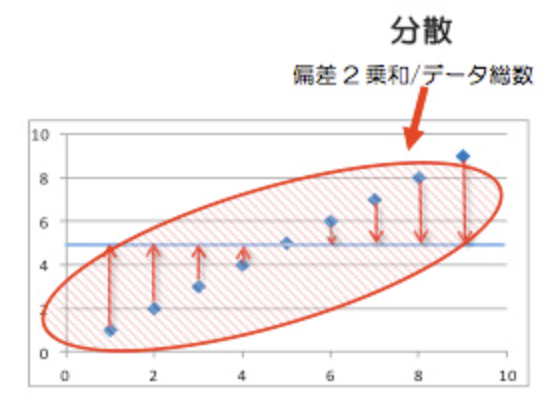
分散
分散は、データの散らばりを指し、その数値が大きければ大きいほど、データ全体の散らばりが大きいことを意味します。つまりは、個々の偏差を平均を表したものということですね。
出典:「なるほど統計学園」https://www.stat.go.jp/naruhodo/10_tokucho/chirabari.html
標準偏差
標準偏差は分散と同様に、データの散らばりを指し、その数値が大きければ大きいほど、データ全体の散らばりが大きいことを意味します。では、分散と標準偏差は同じなのかというと、指している内容は同じですが、分散は計算の過程で数値を2乗しており本来のデータと単位が異なってしまっています。そのため、分散を標準偏差にすることで、本来のデータと同じ単位にすることができるというわけです。使い分けについては、分散は統計や数学での計算に適しています。その一方で、標準偏差はよりわかりやすくしたものと思ってもらえればと思います。
ちなみに、よく聞く偏差値というのは、平均と標準偏差を利用して、平均が50、標準偏差が10になるように調節して求めたものです。これはよりわかりやすくしたものと思ってもらえればと思います。
まとめ
今回は定期試験のデータの見方として、平均について、そして平均以外でのデータの見方について話しました。
平均とは、集めたデータの数値を全て足したものをその個数で割った値
偏差とは、個々の数値と平均の差の値
分散とは、データの散らばりの値
標準偏差とは、データの散らばりの値
(分散と標準偏差は単位が異なるだけで指している内容は同じ)
ただ単に平均を見ただけでは見えない部分がありますね。これらの数値も参考にしながら、ヒストグラムも作成すると、より全体のばらつきを見ることができますね。もし平均だけでしかテストのデータを見ていないという人は是非これらの数値でもデータを分析してみましょう。ExcelやGoogleスプレッドシートを使えば難しい計算をしなくても簡単に値を求めてくれます。
次回は平均点60というものが何故求められるか考えることができればと思います。
また、今回は計算方法等は省き、その数値が何を指しているかだけを説明しましたが、もし計算方法やさらに詳しく知りたい人は「なるほど統計学園」に是非アクセスしてみてください。
皆さんの実践や研究の少しでも役に立てば幸いです。Tomorrow is another day.
Last Updated on 2022年7月9日




コメント